Penjumlahan dan Pengurangan Matriks

klik di sini!! matriks movie.rar

Asal Usul Angka

Posted: November 17, 2011 in Math Fun, Math News
Tags: matematika fun, math info
 

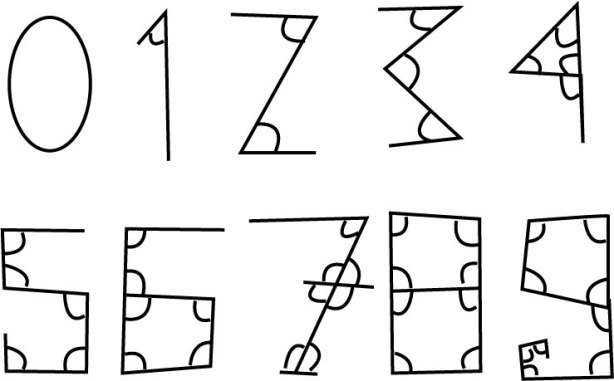
sudah lama tidak posting….ini ada sedikit bahan yang cukup menarik mengenai asal usul angka………….ternyata angka pertama kali diciptaan berdasarkan banyaknya sudut seperti gambar berikut ini.

semoga bermanfaat…..:-)

Pangkat 0

Posted: December 31, 2010 in Math Fun, Math News
Tags: matematika fun, math info
 

sharing sedikit tentang perpangkatan…..terutama tentang pangkat 0 (nol)…..sudah banyak orang tau tentang pangkat, misalnya 2 pangkat 3 ditulisnya 2^3…..artinya 2 x 2 x 2 = 8…..disini 2 dikalikan dirinya sendiri sebanyak pangkatnya, yaitu 3…..tapi gimana kalau 2 dipangkatkan 0 (nol)…..apakah 2 dikalikan dirinya sendiri sebanyak 0 (nol) kali…..???jadinya berapa donk…..???

ternyata ga gitu kawand…..begini ceritanya, coba kita ambil contoh lain dulu, misalnya 2^5 : 2^2…..kita hitung dulu 2^5 = 2 x 2 x 2 x 2 x 2 = 32…..kemudian 2^2 = 2 x 2 = 4…..nah jadinya 2^5 : 2^2 = 32 : 4 = 8…..kalau kita perhatiin bilangan 8 ini juga ada hubungannya dengan bilangan awal tadi, yaitu bilangan 2…..8 = 2^3…..nah sekarang bilangan 3 itu dari mana asal muasalnya…..?ternyata dari pangkat atas dikurangin pangkat yang bawah (pangkat pembagi) yaitu 5 – 2 = 3…..untuk bilangan yang lain juga begitu…..dapatlah kita sifat a^m : a^n = a^(m-n)…..

rumus itu bisa kita peroleh dengan coba2 masukin angka…..sekarang kita akan coba masukin angka 2^4 : 2^4 = 2 x 2 x 2 x 2 : 2 x 2 x 2 x 2 = 16 : 16 = 1…..nah disini diperoleh hasilnya 1…..misalkan kita coba lagi 2^3 : 2^3 = 2 x 2 x 2 : 2 x 2 x 2 = 8 : 8 = 1…..dapat hasilnya 1 lagi…..dan lagi kalau kita masukkan pangkat atas bawah sama…..dapet rumus a^n : a^n = 1…..padahal kalau digabung dengan rumus sebelumnya a^n : a^n = a^(n-n) = a^0 = 1…..dapatlah bahwa a^0 = 1…..

Asyik kan…..dengan logika yang sederhana bisa mecahin teka-teki pangkat 0…..sekedar info aja deh…..semoga bermanfaat…..

Keunikan Dibalik Bilangan 12 dan 13

YANG UNIK DARI BILANGAN 12 DAN 13

Tiga belas (13) bukanlah angka sial, ini hanya mytos belaka. Selain tidak logis juga gak ilmiah. Tapi semua kembali ke anda. Dalam matematika ada suatu keunikan tentang bilangan 13.

Tapi dalam masalah ini yang akan saya angkat tentang keunikan bilangan 12 dan 13 serta pengembangannya.

A. Bilangan 12 jika angka dibalik menjadi 21
12^2=144
102^2=10404
1002^2=1004004
10002^2=100040004
100002^2=10000400004
dst
21^2=441
201^2=40401
2001^2=4004001
20001^2=400040001
200001^2=40000400001
dst
112^2=12544
10102^2=102050404
1001002^2=1002005004004
dst 
211^2=44521
20101^2=404050201 
2001002^1=4004005002001
dst
B. Bilangan 13 jika angka dibalik menjadi 31
13^2=169
103^2=10609
1003^2=1006009
10003^2=100060009
100003^2=10000600009
dst
31^2=961
301^2=90601
3001^2=9006001
30001^2=900060001
300001^2=90000600001
dst
113^2=12769
10103^2=102070609
1001003^2=1002007006009
dst 
311^2=06721
30101^2=906070201
3001001^2=9006007002001
dst
yang unik di sini bilangan itu dan bilangan hasil menukar angka akan membentuk pola

 By Andromedha

Pembuktian Rumus Luas Trapesium

Rumus Trapesium

Pembuktian Rumus Luas Trapesium

Trapesiuma adalah segiempat yang memiliki sepasang sisi sejajar. Rumus luas trapesium sudah sangat dikenal oleh anak SD. Akan tetapi rata-rata mereka tidak mengetahui dari mana asalnya. Berikut ini akan kami jabarkan mengapa rumus luas trapesium adalah
L = 0,5 x jumlah sisi sejajar x tinggi




Perhatikan bahwa
b = x + a + y ...........................(1)
L₁ = 0,5 xt ..............................(2)
L₂ = at ....................................(3)
L₁ = 0,5yt ...............................(4)

L_trapesium = L₁ + L₂ + L₃
= 0,5 xt + at + 0,5 yt
= (0,5x + a + 0,5y)t
= 0,5(x + 2a + y)t
= 0,5(a + x + a + y)t
Dengan mensubstitusi persamaan (1) maka diperoleh
L_trapesium = 0,5(a + b) t
= 0,5 x jumlah sisi sejajar x tinggi 

 

Uniknya Matematika

Uniknya matematika

By gamatika 54 Comments

Categories: Math Zone
Tags: gamatika, matematika, universitas mataram

Uniknya Matematika

kita tahu matematika sudah terkesan ngeri/rumit dan menuh-menuhin kapasitas otak kita saja,,apalagi ngeliat angka n rumus-rumusnya,,waduuuuuuuuh tambah pusiiiiing…….

But,,dibalik itu semua ternyata matematika mempunyai sisi unik yang mungkin kita tidak sadar akan hal itu,,di postingan ne,,saya akan menunjukan ke_Unikan matematika dalam hal operasinya, dalam perkalian dan pembagian,,.

• Dalam opersai-operasinya
  
  Disini terdapat keunikan yang mungkin belum pernah kita lihat (bagi yang sudah diem ja ya,,hehehee)
  
  • Penjumlahan unik
    
    
    
    

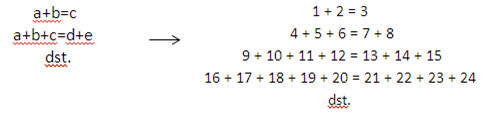
• Kedua bilangan yang berurutan dan saling bertanda kuadrat jika dikurangkan, maka hasilnya sama dengan penjumlahan kedua bilangan tersebut tanpa memperhatikan kuadratnya.
  
  
  
  3²-2² = 3 + 2
  6²-5² = 6 + 5,
  
  
  Dan kawan-kawannya,,
  
• Angka 15.873 jika dikalikan dengan 7 dan kelipatannya, hasilnya akan unik.
  
  15873 x 7 = 111111
  15873 x 14 = 222222
  15873 x 21 = 333333
  15873 x 28 = 444444
  15873 x 35 = 555555; dst
  

(http://www.dodoardiles.co.cc/2010/05/berbicara-tentang-matematika-kali-ini.html)

• Dalam perkalian
  
  Disini saya menemukan beberapa ke_Unikan cara memperoleh hasil perkalian,,
  
  • Neh perkalian pertama yang saya temuin
    
    Sebelumnya mau ngasi tau dulu neh,,perkalian model ne hanya berlaku untuk perkalian belasan ja(10-19),,
    
    Langsung ja,,menuju ke TKP,,.
    
    Trik-triknya sebagai berikut:
    
    Gene neh model umum perkaliannya 1a x 1b,,dimana a dan b tu dari 0 sampai 9,,.
    

1. Langkah awalny,,jumlahkan satuan (b) dengan bilangan di sebelahnya(1a),,ne jadi bilangan ratusan n puluhannya,,.Kita ambil contoh 13 x 12,,Berarti 2 + 13 = 15
   
2. Langkah terakhir sesama satuan dikali,,
   
   Berarti 3 x 2 = 6,,ne jadi satuannya,,Hasil perkalian ne adalah 156,,.
   
   
   
   
   
   
   
   
   

• Neh perkalian kedua
  
  Perkalian kedua ne berlaku jika selain satuannya bilangan yang lainnya sama,,maksudnya puluhan dan ratusannya sama),,dan jumlah satuannya harus 10,,Ne bentuk umumnya,, XXa x XXb dimana X,a dan b bilangan asli dan a + b = 10,,.Saya ambil contoh 56 x 54,,ne triknya brada :
  

1. Kalikan puluhannya dengan bilangan setelahnya dalam urutan bilangan asli,,disini puluhannya 5 berarti 5 dikalikan dengan 6,,ne jadi bilangan bukan satuan n puluhannya,,.
   
   
   
2. Satuannya dikali,, 4 x 6 = 24,,hasil akhir perkalian ne 3024,,.
   
   
   
   
   

• Neh perkalian ketiga
  
  Ne berlaku untuk semua brada,,
  
  Disini saya ambil contoh 123 x 32,,neeh triknya,,Unik,, :
  

1. Kita bentuk perkalian ne seperti pada gambar dibawah ne,,:
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
2. Di jumlahin deh bilangan yang da dalem kotak-kotak kecil tu,,
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   

• Neh perkalian keempat
  
  Yang terakhir ne saya pkir pling mudah,,disni kita hanya pke garis-garis ja,,
  
  Untuk lebih jelasnya,,langsung ke TKP :
  
  322 x 214,,neh saya ambil soal sebarang,,he
  
  Triknya begini brada,,:
  
  322 x 214
  
  
  
  
  
  
  
  
  
  
  
  
  
  Jumlahkan setiap pertemuan antar garis,,seperti pada gambar,,.
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  Setelah semua selesai di jumlahkan,,aturannya sama seperti penjumlahan biasa,,karena dkotak kuning bernilai 10 jadi angka 1 nya berpindah k lingkaran merah,,dlingkaran merah menjadi 19,,begitu seterusnya,,.
  
  
  
  
  
  
  
  Jadi,,hasil perkaliannya adalah 68908,,.
  
  
  

• Dalam pembagian
  
  Dalam pembagian ne saya hanya mendapat ke_Unikan pada pembagian oleh angka 9,,.
  
  Saya ambil contoh 221013 dibagi 9,,Kalu secara manual ne lmyan lamadiselesaikan,,but,,da trik untuk membantu,,Neh tak bocorin triknya,,.221013 dibagi 9
  
  Hasilnya 24557,,nah lo kok bisa langsung gene ya jawabannya,,,hehe
  
  Neh langka-langkahnya,,:
  
  
  
  
  
  
  
  
  
  
  
  Angka pertama selalu tetap,,dalam contoh ne adalah 2,,tanda panah berarti dijumlahkan,,2 + 2 = 4; 4 + 1 = 5;
  
  5 + 0 = 5; 5 + 1 = 6,,untuk 6 + 3 = 9 tidak langsung dituliskanakan tetapi penjumlahan yang terakhir tu dibagi dengan 9,,
  
  9 dibagi 9 = 1,,hasilnya ne ditambahkan ke digit terakhir yaitu 6 + 1 = 7,,
  
  Sehingga hasil akhirnya adalah 24557,,.
  
  
  
  Yah sampe disni ke_Unikan yang saya temukan selama surfing didunia maya,,hehe
  
  Oya,,bagi temen2 yang pengen ngeliat videonya tentang ke_Unikan perkalian n pembagian ne,,dapat kalian liat d akun FB saya,,boris bertynegara milanisti neh kalau emang berminat ngeliat videonya,,
  
  
  

Sebelum berakhir tilisan ne,,saya mau kasi temen2 tebak2an neh,,

Ambil 1000 dan tambahkan 40 padanya. Sekarang tambahkan 1000 lagi. Sekarang tambahkan 30 . !

Tambahkan 1000 lagi . Sekarang tambahkan 20. Sekarang tambahkan 1000

Sekarang tambahkan 10 . Berapa totalnya?

Hayooooooo jawab kalau bisa,,,,,,,,,,,,,,,,,,,,,,

by : Borisman Bertinegara / GID 007 010

Tokoh Matematika Islam

1.    Al Khawarizmi
Al Khawarizmi adalah seorang ahli matematika yang sangat terkenal diseluruh dunia. penemuan paling menakjubkannya adalah tentang rumus matematika yang dimana rumus itu sering menggunakan cara huruf dikalikan dengan angka atau yang biasa disebut dengan Aljabar.

2.    Abu Wafa al Bawzajani

       Salah seorang ahli matematika muslim terbesar. Ia dikenal sebagai ahli astronomi dan pengembang trigonometri (ilmu ukur sudut), dan orang yang pertama yang mengajukan beberapa rumus penting dalam trigonometri. Salah satu rumus yang didedikasikan kepadanya adalah Cos C= Cos a.cos b.

3. Al Kalasadi (abad 9 H/ 15 M)
Seorang pakar fiqih (hukum) dan juga pakar matematika yang inovatif asal Andalusia (Spanyol Islam), pencipta notasi pecahan modern. Komentarnya terhadap Takhlis Ibn Al Banna memuat suatu rumusantingkat tinggi untuk memperoleh akar kwadrat dengan kecermatan dan ketepatan yang nyaris sempurna.
Dalam notasi pecahan, dialah orang pertama yang menggunakan simbol-simbol seperti yang digunakan kini secara luas.

4. Al Halili (abad 8 H/ 14 M)
Seorang pakar matematika dan astronomi. Ia banyak menghasilkan karya matematika dan astronomi ang berbobot tinggi. Ia berasal dari damaskus yang hidup pada abad ke 14 Masehi. Ia menjadi masyhur karena kemampuannya dalam menentukan arah kiblat dengan menyajikan garis-garis bujur dan garis-garis lintangnya dengan bantuan perhitungan rumit matematika. Tabel-tabel kiblatnya merupakan tabel trigonometrik canggih pertama. Ia berhasil mengkonfilasi sebuah tabel kiblat yang distandarkan pada sebuah rumusan canggih dan akurat. Hal ini menggambarkan kompetensi dan ketinggian otorotas kecendikiawannya dalam aljabar fungsi dan tekhnik-tekhnik komputansi.